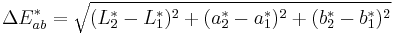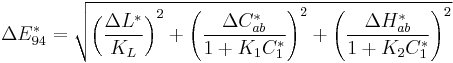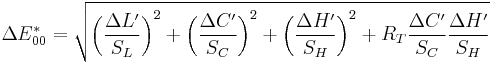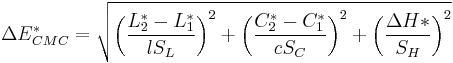Color difference

The difference or distance between two colors is a metric of interest in color science. It allows people to quantify a notion that would otherwise be described with adjectives, to the detriment of anyone whose work is color critical. Common definitions make use of the Euclidean distance in a device independent color space.

1 Delta E
2 Tolerance
3 Footnotes
4 Further reading
5 External links

Delta E

The International Commission on Illumination (CIE) calls their distance metric ΔE^*_ab (also called ΔE*, dE*, dE, or “Delta E”) where delta is a Greek letter often used to denote difference, and E stands for Empfindung; German for "sensation". Use of this term can be traced back to the influential Hermann von Helmholtz and Ewald Hering.^[1]^[2]

In theory, a ΔE of under 1.0 is supposed to be indistinguishable unless the samples are adjacent to one another.^[3] However, perceptual non-uniformities in the underlying CIELAB color space prevent this and have led to the CIE's refining their definition over the years.^[4] These non-uniformities are important because the human eye is more sensitive to certain colors than others. A good metric should take this into account in order for the notion of a "just noticeable difference" to have meaning. Otherwise, a certain ΔE that may be insignificant between two colors that the eye is insensitive to may be conspicuous in another part of the spectrum.^[5]

CIE76

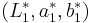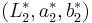Using $({L^*_1},{a^*_1},{b^*_1})$ and $({L^*_2},{a^*_2},{b^*_2})$ , two colors in L*a*b*:

$\Delta E_{ab}^* = \sqrt{ (L^*_2-L^*_1)^2%2B(a^*_2-a^*_1)^2 %2B (b^*_2-b^*_1)^2 }$

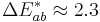$\Delta E_{ab}^* \approx 2.3$ corresponds to a JND (just noticeable difference).^[6]

CIE94

The 1976 definition was extended to address perceptual non-uniformities, while retaining the L*a*b* color space, by the introduction of application-specific weights derived from an automotive paint test's tolerance data.^[7]

ΔE (1994) is defined in the L*C*h* color space with differences in lightness, chroma and hue calculated from L*a*b* coordinates. Given a reference color^[8] 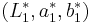$(L^*_1,a^*_1,b^*_1)$ and another color 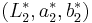$(L^*_2,a^*_2,b^*_2)$ , the difference is:^[9]^[10]^[11]

$\Delta E_{94}^* = \sqrt{ \left(\frac{\Delta L^*}{K_L}\right)^2 %2B \left(\frac{\Delta C^*_{ab}}{1%2BK_1 C^*_1}\right)^2 %2B \left(\frac{\Delta H^*_{ab}}{1%2BK_2 C^*_1}\right)^2 }$

where:

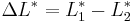
$\Delta L^* = L^*_1 - L^*_2$

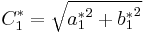
$C^*_1 = \sqrt{ {a^*_1}^2 %2B {b^*_1}^2 }$

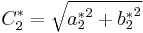
$C^*_2 = \sqrt{ {a^*_2}^2 %2B {b^*_2}^2 }$

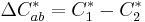
$\Delta C^*_{ab} = C^*_1 - C^*_2$

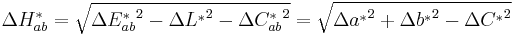
$\Delta H^*_{ab} = \sqrt{ {\Delta E^*_{ab}}^2 - {\Delta L^*}^2 - {\Delta C^*_{ab}}^2 } = \sqrt{ {\Delta a^*}^2 %2B {\Delta b^*}^2 - {\Delta C^*}^2 }$

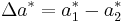
$\Delta a^* = a^*_1 - a^*_2$

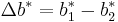
$\Delta b^* = b^*_1 - b^*_2$

and where the weighting factors K depend on the application:

	graphic arts	textiles
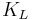$K_L$	1	2
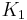$K_1$	0.045	0.048
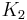$K_2$	0.015	0.014

CIEDE2000

Since the 1994 definition did not adequately resolve the perceptual uniformity issue, the CIE refined their definition, adding five corrections:^[12]^[13]

A hue rotation term (R_T), to deal with the problematic blue region (hue angles in the neighborhood of 275°):^[14]
Compensation for neutral colors (the primed values in the L*C*h differences)
Compensation for lightness (S_L)
Compensation for chroma (S_C)
Compensation for hue (S_H)

$\Delta E_{00}^* = \sqrt{ \left(\frac{\Delta L'}{S_L}\right)^2 %2B \left(\frac{\Delta C'}{S_C}\right)^2 %2B \left(\frac{\Delta H'}{S_H}\right)^2 %2B R_T \frac{\Delta C'}{S_C}\frac{\Delta H'}{S_H} }$

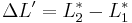
$\Delta L^\prime = L^*_2 - L^*_1$

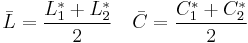
$\bar{L} = \frac{L^*_1 %2B L^*_2}{2} \quad \bar{C} = \frac{C^*_1 %2B C^*_2}{2}$

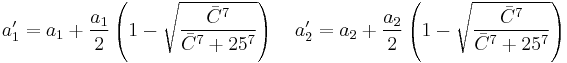
$a_1^\prime = a_1 %2B \frac{a_1}{2} \left( 1 - \sqrt{\frac{\bar{C}^7}{\bar{C}^7 %2B 25^7}} \right) \quad a_2^\prime = a_2 %2B \frac{a_2}{2} \left( 1 - \sqrt{\frac{\bar{C}^7}{\bar{C}^7 %2B 25^7}} \right)$

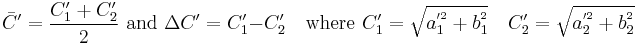
$\bar{C}^\prime = \frac{C_1^\prime %2B C_2^\prime}{2} \mbox{ and } \Delta{C'}=C'_1-C'_2 \quad \mbox{where } C_1^\prime = \sqrt{a_1^{'^2} %2B b_1^{^2}} \quad C_2^\prime = \sqrt{a_2^{'^2} %2B b_2^{^2}} \quad$

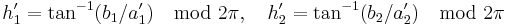
$h_1^\prime=\tan^{-1} (b_1/a_1^\prime) \mod 2\pi, \quad h_2^\prime=\tan^{-1} (b_2/a_2^\prime) \mod 2\pi$

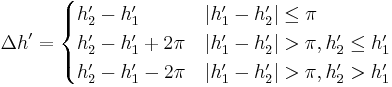
$\Delta h' = \begin{cases} h_2^\prime - h_1^\prime & \left| h_1^\prime - h_2^\prime \right| \leq \pi \\ h_2^\prime - h_1^\prime %2B 2\pi & \left| h_1^\prime - h_2^\prime \right| > \pi, h_2^\prime \leq h_1^\prime \\ h_2^\prime - h_1^\prime - 2\pi & \left| h_1^\prime - h_2^\prime \right| > \pi, h_2^\prime > h_1^\prime \end{cases}$

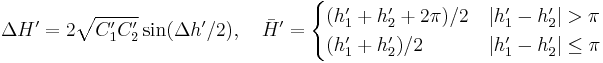
$\Delta H^\prime = 2 \sqrt{C_1^\prime C_2^\prime} \sin (\Delta h^\prime/2), \quad \bar{H}^\prime=\begin{cases} (h_1^\prime %2B h_2^\prime %2B 2\pi)/2 & \left| h_1^\prime - h_2^\prime \right| > \pi \\ (h_1^\prime %2B h_2^\prime)/2 & \left| h_1^\prime - h_2^\prime \right| \leq \pi \end{cases}$

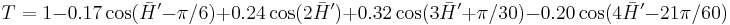
$T = 1 - 0.17 \cos ( \bar{H}^\prime - \pi/6 ) %2B 0.24 \cos (2\bar{H}^\prime) %2B 0.32 \cos (3\bar{H}^\prime %2B \pi/30 ) - 0.20 \cos (4\bar{H}^\prime - 21 \pi/60)$

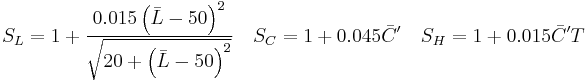
$S_L = 1 %2B \frac{0.015 \left( \bar{L} - 50 \right)^2}{\sqrt{20 %2B {\left(\bar{L} - 50 \right)}^2} } \quad S_C = 1%2B0.045 \bar{C}^\prime \quad S_H=1%2B0.015 \bar{C}^\prime T$

$R_T = -2 \sqrt{\frac{\bar{C}'^7}{\bar{C}'^7%2B25^7}} \sin \left[ \frac{\pi}{6} \exp \left( -\left[ \frac{\bar{H}'-275^\circ}{25} \right]^2 \right) \right]$

CMC l:c (1984)

In 1984, the Colour Measurement Committee of the Society of Dyers and Colourists defined a difference measure, also based on the L*C*h color model. Named after the developing committee, their metric is called CMC l:c. The quasimetric has two parameters: lightness (l) and chroma (c), allowing the users to weight the difference based on the ratio of l:c that is deemed appropriate for the application. Commonly-used values are 2:1^[15] for acceptability and 1:1 for the threshold of imperceptibility.

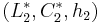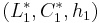The distance of a color $(L^*_2,C^*_2,h_2)$ to a reference $(L^*_1,C^*_1,h_1)$ is:^[16]

$\Delta E^*_{CMC} = \sqrt{ \left( \frac{L^*_2-L^*_1}{l S_L} \right)^2 %2B \left( \frac{C^*_2-C^*_1}{c S_C} \right)^2 %2B \left( \frac{\Delta H*}{S_H} \right)^2 }$

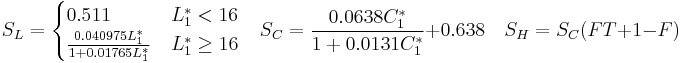
$S_L=\begin{cases} 0.511 & L^*_1 < 16 \\ \frac{0.040975 L^*_1}{1%2B0.01765 L^*_1} & L^*_1 \geq 16 \end{cases} \quad S_C=\frac{0.0638 C^*_1}{1%2B0.0131 C^*_1} %2B 0.638 \quad S_H=S_C (FT%2B1-F)$

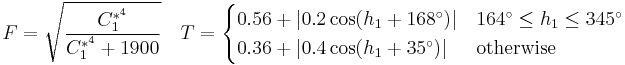
$F = \sqrt{\frac{C^{*^4}_1}{C^{*^4}_1%2B1900}} \quad T=\begin{cases} 0.56 %2B |0.2 \cos (h_1%2B168^\circ)| & 164^\circ \leq h_1 \leq 345^\circ \\ 0.36 %2B |0.4 \cos (h_1%2B35^\circ) | & \mbox{otherwise} \end{cases}$

CMC l:c is designed to be used with D65 and the CIE Supplementary Observer.^[17]

Tolerance

Tolerancing concerns the question "What is a set of colors that are imperceptibly/acceptably close to a given reference?" If the distance measure is perceptually uniform, then the answer is simply "the set of points whose distance to the reference is less than the just-noticeable-difference (JND) threshold." This requires a perceptually uniform metric in order for the threshold to be constant throughout the gamut (range of colors). Otherwise, the threshold will be a function of the reference color—useless as an objective, practical guide.

In the CIE 1931 color space, for example, the tolerance contours are defined by the MacAdam ellipse, which holds L* (lightness) fixed. As can be observed on the diagram on the right, the ellipses denoting the tolerance contours vary in size. It is partly due to this non-uniformity that lead to the creation of CIELUV and CIELAB.

More generally, if the lightness is allowed to vary, then we find the tolerance set to be ellipsoidal. Increasing the weighting factor in the aforementioned distance expressions has the effect of increasing the size of the ellipsoid along the respective axis.^[18]

Footnotes

^ http://books.google.com/books?id=DrduOSrOFegC&pg=PA188&lpg=PA188&dq=(grundempfindung%7Cempfindung)+helmholtz+color&source=web&ots=g_T3sFQ7eG&sig=4HBhygBAc3zW-XfGVPlaykl72bA
^ http://books.google.com/books?id=OoESifAi9ZsC&pg=PA278&lpg=PA278&dq=empfindung+color&source=web&ots=-z6JbcN54V&sig=-Bww3AcNWpnDQp1Lu7yqGBFyUOw
^ Humans have an acute ability of detecting difference by comparison
^ Real World Color Management, Second Edition (Bruce Fraser)
^ Evaluation of the CIE Color Difference Formulas
^ Gaurav Sharma (2003). Digital Color Imaging Handbook (1.7.2 ed.). CRC Press. ISBN 084930900X. http://books.google.com/?id=OxlBqY67rl0C&pg=PA31&vq=1.42&dq=jnd+gaurav+sharma.
^ "Delta E: The Color Difference". Colorwiki.com. http://www.colorwiki.com/wiki/Delta_E:_The_Color_Difference. Retrieved 2009-04-16.
^ Called such because the operator is not commutative. This makes it a quasimetric.
^ Bruce Justin Lindbloom. "Delta E (CIE 1994)". Brucelindbloom.com. http://www.brucelindbloom.com/Eqn_DeltaE_CIE94.html. Retrieved 2011-03-23.
^ "Colour Difference Software by David Heggie". Colorpro.com. 1995-12-19. http://www.colorpro.com/info/software/heggie.html. Retrieved 2009-04-16.
^ "CIE 1976 L*a*b* Colour space draft standard". http://www.physics.kee.hu/cie/newcie/nc/DS014-4_3.pdf. Retrieved 2011-03-23.
^ Sharma, Gaurav; Wencheng Wu, Edul N. Dalal (2005). "The CIEDE2000 color-difference formula: Implementation notes, supplementary test data, and mathematical observations". Color Research & Applications (Wiley Interscience) 30 (1): 21–30. doi:10.1002/col.20070. http://www.ece.rochester.edu/~gsharma/ciede2000/ciede2000noteCRNA.pdf.
^ Bruce Justin Lindbloom. "Delta E (CIE 2000)". Brucelindbloom.com. http://www.brucelindbloom.com/Eqn_DeltaE_CIE2000.html. Retrieved 2009-04-16.
^ The "Blue Turns Purple" Problem, Bruce Lindbloom
^ Meaning that the lightness contributes half as much to the difference (or, identically, is allowed twice the tolerance) as the chroma
^ Bruce Justin Lindbloom. "Delta E (CMC)". Brucelindbloom.com. http://www.brucelindbloom.com/Eqn_DeltaE_CMC.html. Retrieved 2009-04-16.
^ CMC
^ http://www.xrite.com/documents/literature/en/L10-024_Color_Tolerance_en.pdf

External links

Mauro Boscarol color difference calculator. Implementation in Adobe AIR
Bruce Lindbloom's color difference calculator. Uses all metrics defined herein.
The CIEDE2000 Color-Difference Formula, by Gaurav Sharma. Implementations in MATLAB and Excel.
Color Similarity Tool, by Dragan Bajcic, Implementations in PHP and Javascript.
python-colormath. Implementation in Python.
Precise Color Communication Konica Minolta Sensing.